1. Задание № 202 

Сложность: III
Классификатор алгебры: 5\.2\. Неравенства первой и второй степени относительно логарифмических функций
Логарифмические неравенства
i
Найдите сумму наименьшего и наибольшего целых решений неравенства 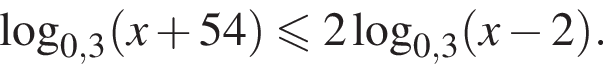
Решение. Найдем область определения неравенства:
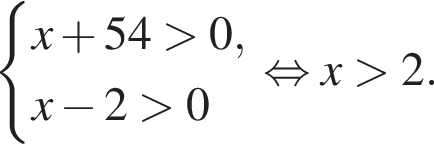
На ОДЗ имеем:
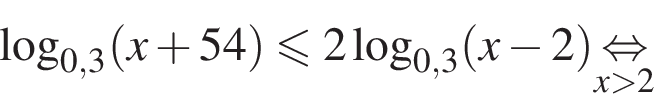
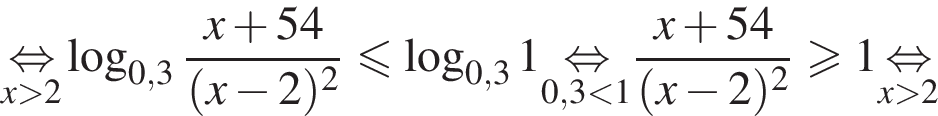
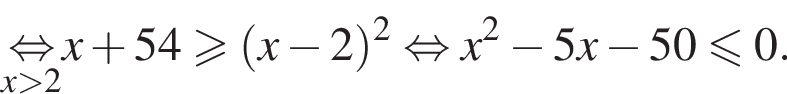
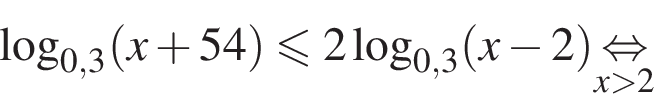
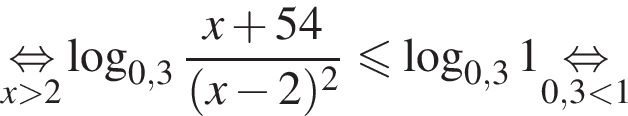
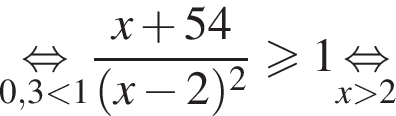
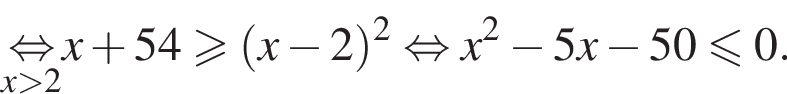
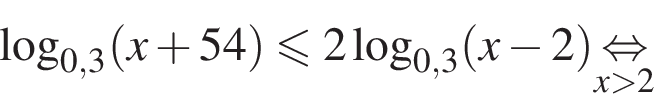
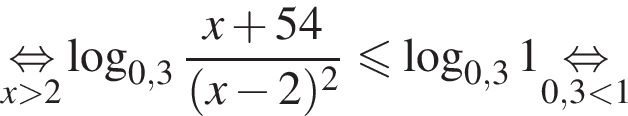
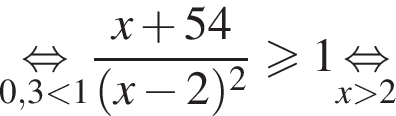

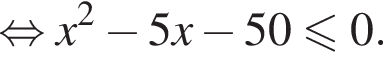
Поэтому в силу ![]() :
: 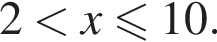 Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.
Наименьшим целым решением неравенства является число 3, наибольшим целым решением — число 10, их сумма равна 13.
Ответ: 13.
Ответ: 13
202
13
Сложность: III
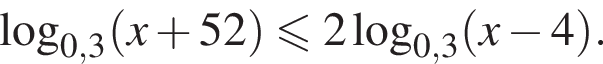
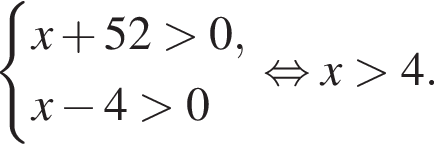
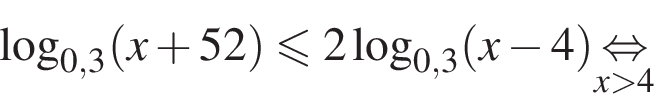
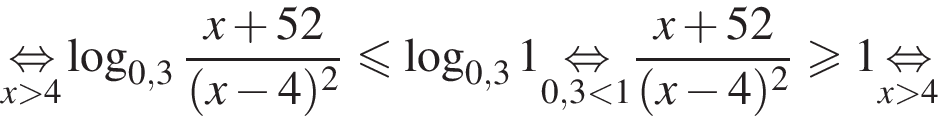
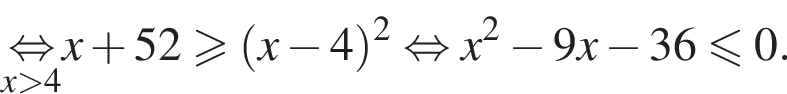
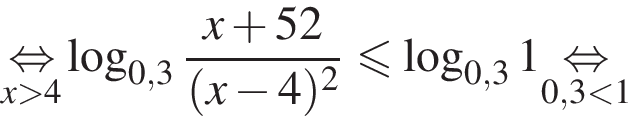
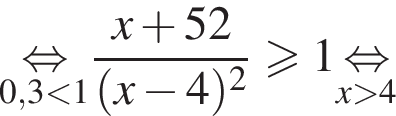
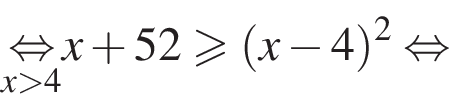
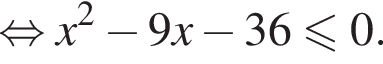
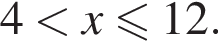 Наименьшее целое решение неравенства — число 5, наибольшее целое решение — число 12, их сумма равна 17.
Наименьшее целое решение неравенства — число 5, наибольшее целое решение — число 12, их сумма равна 17.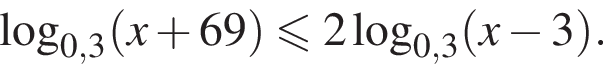
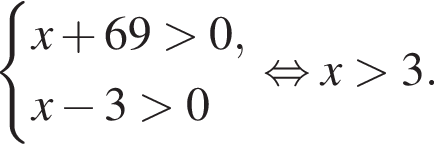
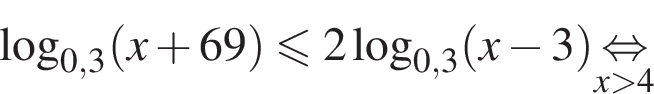
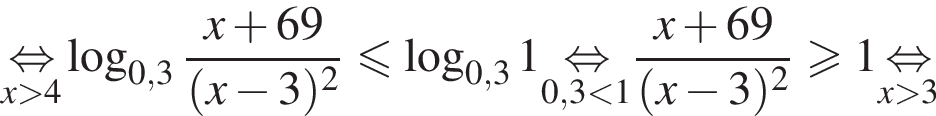
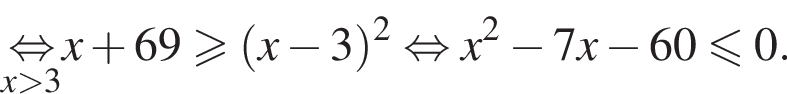
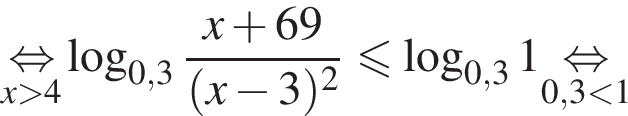
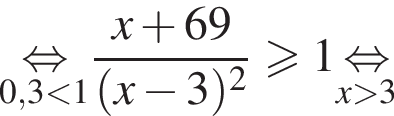
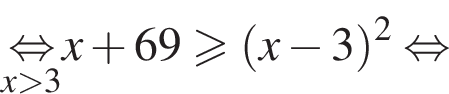
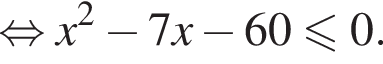
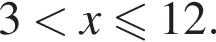 Наименьшее целое решение неравенства — число 4, наибольшее целое решение — число 12, их сумма равна 16.
Наименьшее целое решение неравенства — число 4, наибольшее целое решение — число 12, их сумма равна 16.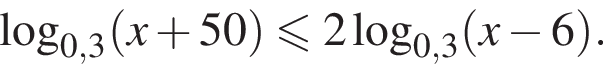
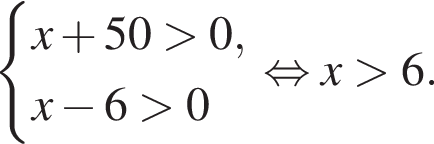
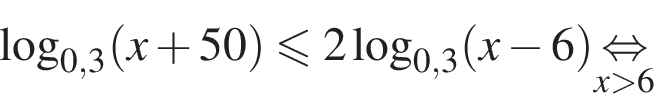
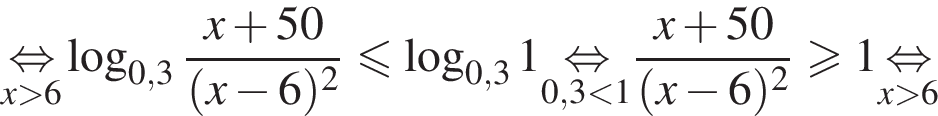
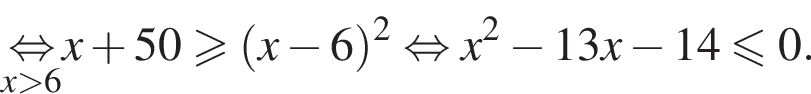
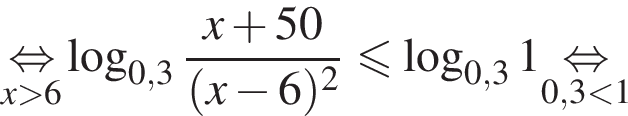
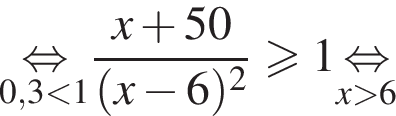
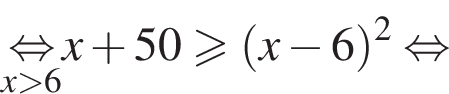
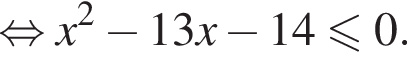
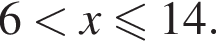 Наименьшее целое решение неравенства — число 7, наибольшее целое решение — число 14, их сумма равна 21.
Наименьшее целое решение неравенства — число 7, наибольшее целое решение — число 14, их сумма равна 21.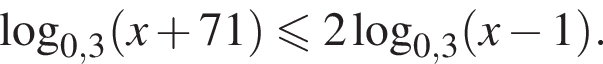
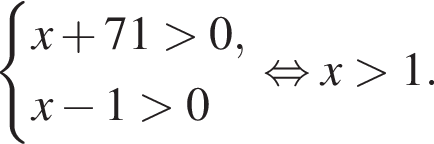
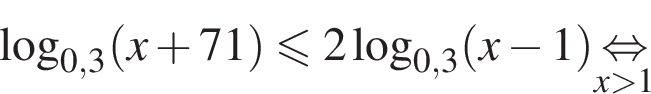
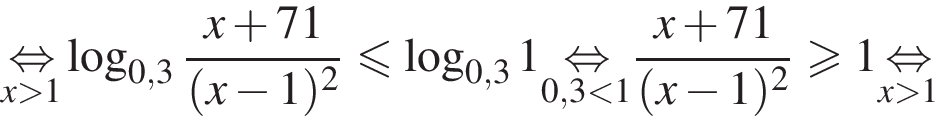
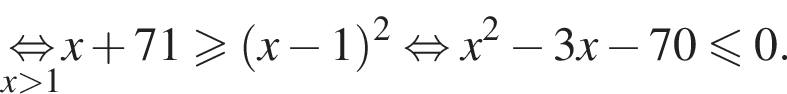
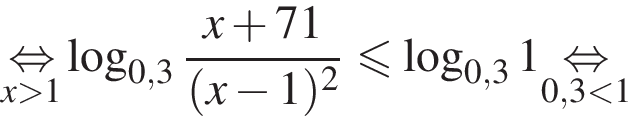
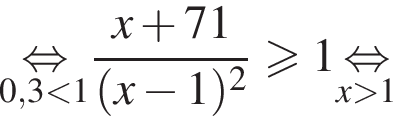
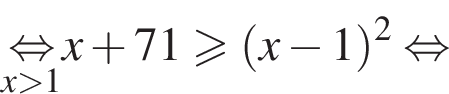
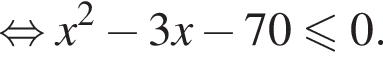
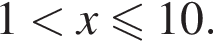 Наименьшее целое решение неравенства — число 2, наибольшее целое решение — число 10, их сумма равна 12.
Наименьшее целое решение неравенства — число 2, наибольшее целое решение — число 10, их сумма равна 12.